本文最后更新于 2026-01-10T16:27:24+08:00
这是一道回滚莫队的例题,欢迎来看我的莫队博客。
在看本题题解之前,请先自行了解普通莫队。
有些题目在区间转移时,可能会出现增加或者删除无法实现的问题。在只有增加不可实现或者只有删除不可实现的时候,就可以使用回滚莫队在
$O(n \sqrt m)$
的时间内解决问题。回滚莫队的核心思想就是:既然只能实现一个操作,那么就只使用一个操作,剩下的交给回滚解决。
形式化:给你一个长度为 n
的数组 A 和 m 个询问 (1 ≤ n, m ≤ 105),每次询问一个区间
[L, R]
内重要度最大的数字,要求:输出其重要度。一个数字
i
重要度的定义为 i 乘上 i 在区间内出现的次数。
在这个问题中,在增加的过程中更新答案是很好实现的,就直接使用新增元素乘上出现次数去更新答案就可以解决,但是在删除的过程中更新答案是不好实现的。因为如果增加会影响答案,那么新答案必定是刚刚增加的数字的重要度,而如果删除过后区间重要度最大的数字改变,我们很难确定新的重要度最大的数字是哪一个。
于是使用回滚莫队,我们像普通莫队一样分块,排序,并设块的大小为 b。
对于每堆左端点在同一个块内的询问,我们分别进行考虑,这时的莫队区间的左端点初始化为这个块的右端点加
1,将莫队区间的右端点初始化为这个块的右端点。
对于左右端点在同一个块中的询问,我们直接暴力扫描回答即可(这个显然是
O(b) 的)。
对于这堆询问中的每一个询问,不断扩展右端点直至莫队区间的右端点等于询问的右端点,因为右端点是排过序的,所以右端点的移动是
O(n) 的。
然后定义一个操作撤销,具体的,在这道题中指在桶中减去出现次数,而不管答案是否改变,并将答案使用原来的答案覆盖(相当于回到之前某一个时刻的状态)。
对于每一个块内的询问,具体的算法流程如下:
先更新右端点(向右移动)。我们将现在莫队的状态称为基准状态。
暴力向左找,不断扩展莫队区间的左端点直至莫队区间的左端点等于询问的左端点。
回答询问(记录答案)。
撤销莫队区间左端点的改动,使莫队区间的左端点回滚到这个块的右端点加
1。也就是回到基准状态。其实如果你用状态覆盖去理解是可以的,但是暴力覆盖状态是
Θ(n)
的,我们发现其实只有最多 b
个元素(块的右端点到询问左端点)更改了,直接对于这几个元素修改回去就可以
Θ(b)
回滚了。
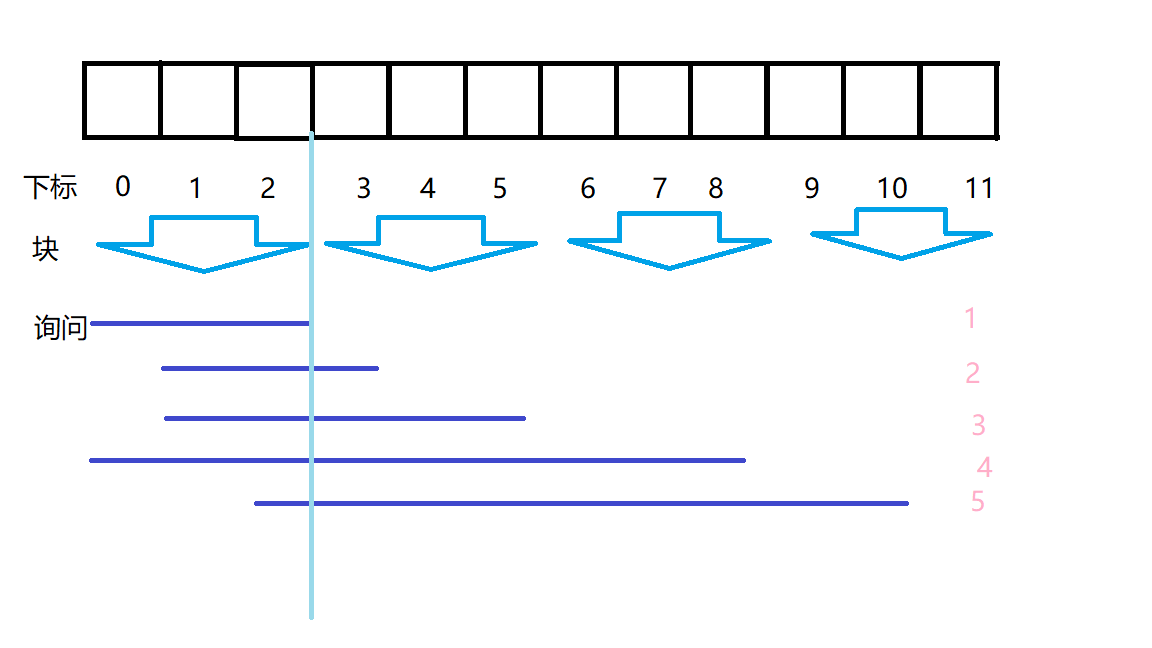
具体来分析吧。
对于 1 号询问,由于就是在块内,所以暴力处理。
对于 2 号询问,莫队区间先是右端点从 2 扩展到 3,然后左端点扩展到
1,记录答案,左端点重新回到 3。
对于 3 号询问,莫队区间先是右端点从 3 扩展到 5,然后左端点从 3 来到
1,记录答案,左端点重新回到 3。
对于 4 号询问,莫队区间先是右端点从 5 扩展到 8,然后左端点从 3 来到
0,记录答案,左端点重新回到 3。
对于 5 号询问,莫队区间先是右端点从 8 扩展到 10,然后左端点从 3 来到
2,记录答案,左端点重新回到 3。
时间复杂度是 $O(mb+\frac{n^2}{b})$,取 $b=\frac{n}{\sqrt{m}}$ 最优,时间复杂度为
$O(n\sqrt{m})$。
最优解倒二:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
| #include<bits/stdc++.h>
#ifndef ONLINE_JUDGE
#define __gcd gcd
#endif
using namespace std;
int a[100000 + 10];
long long sum, lst;
unordered_map<int, int>vis;
void add(int x) {
vis[a[x]]++;
sum = max(sum, vis[a[x]] * 1ll * a[x]);
}
int n, Q, bel[100000 + 10], R[100000 + 10];
struct query {
int l, r, id; long long ans;
friend bool operator<(const query& a, const query& b) {
return bel[a.l] == bel[b.l] ? a.r < b.r : bel[a.l] < bel[b.l];
}
}q[100000 + 10];
signed main() {
cin.tie(0)->sync_with_stdio(false);
cin >> n >> Q;
for (int i = 1; i <= n; ++i) cin >> a[i];
int t1 = 0, t2 = pow(n, 0.5), t3 = 1;
for (int i = 1; i <= n; ++i) {
bel[i] = t3;
t1++;
if (t1 == t2) R[t3] = i, t1 = 0, t3++;
}
for (int j = 1; j <= Q; ++j) cin >> q[j].l >> q[j].r, q[j].id = j;
sort(q + 1, q + Q + 1);
int r = 0;
for (int j = 1; j <= Q; ++j) {
if (bel[q[j - 1].l] ^ bel[q[j].l]) {
unordered_map<int, int>().swap(vis);
sum = 0;
while (bel[q[j].r] == bel[q[j].l]) {
for (int i = q[j].l; i <= q[j].r; ++i) add(i);
q[j].ans = sum;
unordered_map<int, int>().swap(vis);
sum = 0;
if (bel[q[j].l] ^ bel[q[j + 1].l]) break;
j++;
}
if ((bel[q[j].l] ^ bel[q[j + 1].l]) && bel[q[j].r] == bel[q[j].l]) continue;
r = R[bel[q[j].l]] + 1;
add(r);
}
1;
while (r < q[j].r) add(++r);
lst = sum;
int l = R[bel[q[j].l]]; add(l);
while (l > q[j].l) add(--l);
q[j].ans = sum;
while (l <= R[bel[q[j].l]]) vis[a[l]]--, l++;
sum = lst;
}
sort(q + 1, q + Q + 1, [](const query& a, const query& b)->bool {return a.id < b.id; });
for (int i = 1; i <= Q; ++i) cout << q[i].ans << endl;
return 0;
}
|
