网络流

定义

网络流是什么呢？举个形象点的例子：

假设有这么一个班，他们有无穷个人，他们每个人都要去以光速抢饭~~（符合现实）~~，但是由于人太多了，每个楼道都会人挤人，所以每条楼道都有一个同时容纳人数限制，问同时会有多少人第一时间赶到食堂吃饭。

还是太抽象了，我们来看一个更具体的例子。

我们想象一下自来水厂到你家的水管网是一个复杂的有向图，每一节水管都有一个最大承载流量。现在自来水厂拼命的往管网里面注水，但你家收到的水流量也是有上限的（毕竟每根水管承载量有限）。你想知道你能够拿到多少水。

最大流

Ford–Fulkerson 增广

Ford–Fulkerson 增广是计算最大流的一类算法的总称。该方法运用贪心的思想，通过寻找增广路来更新并求解最大流。

现在我们定义一个新定义为剩余流量，它是一条边的最大流量减去当前流量。

现在我们把每一条边都反向建一条边，约定 $(u,v)$ 的流量等于 $(v,u)$ 的流量的相反数，而且 $f(u, v)$ 增加时 $f(v, u)$ 应当减少同等的量。

注意到有流量的数值可能为负，所以我们把每条剩余流量大于 $0$ 的边都单独拎出来，再加上所有点，构成残量网络 $G_f$，它代表着这里面的边都是可以继续增加流量的，即 $G_f=(V,E_f)$，其中 $E_f=\{(u,v) \mid c_f(u,v)>0\}$。

这是什么意思呢，实际上，它代表着「反悔和抵消」。

现在来看它的思路。

每次我们从残量网络中寻找一条路径，它从源点开始，到汇点结束，我们称之为增广路，我们把它里面每一条边都增加 $1$ 的流量，直到残量网络中再也找不到这样的路径了。

容易发现每次我们都使整张图的流量增加了，但是我们怎么证明这个算法是正确的呢？

这时，我们先假设它是对的，我们可以得出最后残量网络肯定没有从源点开始，到汇点结束的路径了，也就是说老师把学生的路堵完了，学生无路可走了现在是一个割。那么我们每次都是一个一个减少的，所以我们就是得到的最小割。

我们惊奇的发现，FF 增广的正确性与最大流最小割定理（对于任意网络 $G = (V, E)$，其上的最大流 $f$ 和最小割 $\{S, T\}$ 总是满足 $|f| = ||S, T||$）互为充要条件，所以我们直接证明最大流最小割定理。

先思考一个引理：对于网络 $G = (V, E)$，任取一个流 $f$ 和一个割 $\{S, T\}$，总是有 $|f| \leq ||S, T||$，其中等号成立当且仅当 $\{(u, v) | u \in S, v \in T\}$ 的所有边均满流，且 $\{(u, v) | u \in T, v \in S\}$ 的所有边均空流。

证明一下，发现确实不难证，然后我们考虑对于一张任意的网络，它的残量网络在删完后的样子。现在取两个点一端在残量网络中从源点出发可以到达，另一端不行，可以发现，只有两种边，一种正向边，一种反向边，但是它们的残量均为 $0$。

• 对于正向边（$(u,v)$），有 $c(u, v) = f(u, v)$，即 $\{(u, v) \mid u \in S, v \in T\}$ 的所有边均满流；
• 对于反向边（$(v,u)$），$c_f(u, v) = c(u, v) - f(u, v) = 0 - f(u, v) = f(v, u) = 0$，即 $\{(v, u) \mid u \in S, v \in T\}$ 的所有边均空流。

Edmonds–Karp 算法

显然，我们需要寻找增广路，但是我们不知道怎么找，于是我们就暴力 BFS，每次减去流量的最小值。

这就是 EK 算法，时间复杂度是 $O(|V||E|^2)$。

Dinic 算法

EK 还是太暴力了，而且每次遍历一整个残量网络只能找到一条增广路，效率太低，但是如果我们尝试在一次遍历中找到多个增广路如何呢？

首先，我们先对残量网络进行 BFS 分层（即 $d(i)$ 为从源点到 $i$ 所经过的最少边数），然后我们进行 DFS 找增广路，但是 DFS 时有限制，每次只能找下一层的节点（$d(v)=d(u)+1$），我们找到最大的一条增广路，把他删去流量最小值。

但是，有人就问了，你这丝毫优化没有啊？虽然它看起来就没什么优化，但实际上，它确实没有优化。

bool bfs() {
	queueq;
	for (int i = 1; i <= n; ++i) dis[i] = inf;
	dis[s] = 0; q.push(s); bool flg = 0;
	while (!q.empty()) {
		int now = q.front(); q.pop();
		flg |= now == t;
		for (int i = head[now]; i; i = edge[i].nxt) {
			int& v = edge[i].v;
			if (dis[v] == inf && edge[i].w > 0)
				q.push(v), dis[v] = dis[now] + 1;
		}
	}
	return flg;
}

那怎么办？注意到，我们 DFS 时有可能多次尝试同一个点的已经没有可能的边，导致时间复杂度原地起飞，于是我们想要优化尝试过程，减少无意义枚举。

于是，当前弧优化就出现了，它维护 $u$ 的出边表中第一条还有必要尝试的出边，可以证明，加入当前弧优化后，Dinic 算法的时间复杂度是 $O(|V|^2|E|)$。

int dfs(int x, int flow) {
	if (x == t) return flow;
	int ans = 0;
	for (int& i = cur[x]; i; i = edge[i].nxt) {
		int& v = edge[i].v;
		if (edge[i].w > 0 && dis[v] == dis[x] + 1) {
			int k = dfs(v, min(flow, edge[i].w));
			if (k == 0) dis[v] = inf;
			edge[i].w -= k;
			edge[i ^ 1].w += k;
			ans += k; flow -= k;
		}
	}
	return ans;
}

在这里，由于 $\overset{\small\texttt{Count Leading Zeros}}{\texttt{计算前导零的个数}}$ 说可以留到给你们证，我在这里给出伪证一例：

对于每个结点，我们维护下一条可以增广的边，而当前弧最多变化 $|E|$ 次，从而单轮增广的最坏时间复杂度为 $O(|V||E|)$。

而且 Dinic 算法的增广轮数是 $O(|V|)$ 的。考虑反证。假设层次图的层数在一轮增广结束后较原先相等，则层次图上应仍存在至少一条从 $s$ 到 $t$ 的增广路满足相邻两点间的层数差为 $1$。这条增广路未被增广说明该轮增广尚未结束。为了不产生上述矛盾，原命题成立。

所以，Dinic 算法的时间复杂度是 $O(|V|^2|E|)$。

求解二分图最大匹配

实际上，我们将所有边容量均为 $1$ 的网络 $G = (V, E)$，称为是单位容量的。

在单位容量的网络中：

• Dinic 算法的单轮增广的时间复杂度为 $O(|E|)$。

• Dinic 算法的总增广轮数是不会超过 $\min(|E|^{\frac{1}{2}},|V|^{\frac{2}{3}})$ 的。

证明：

先证明单论增广的时间复杂度吧。

发现由于每条边容量均为 $1$，所以增广完就直接没了，每条边只会增广 $1$ 次。

接着证一下总增广轮数 $\le |E|^{\frac{1}{2}}$ 吧。

首先，我们考虑现在我们已经进行了 $|E|^{\frac{1}{2}}$ 次增广。那么至少有一层（一个分层图上的层） $k$ 的出边少于 $|E|^{1-\frac{1}{2}}=|E|^{\frac{1}{2}}$ 条（详情参见抽屉原理）。于是前面 $k$ 层的所有点和它的补集构成了一个割。而且由于最大流最小割定理，$G_f$ 上的最大流不超过 $|E|^{\frac{1}{2}}$。

最后还有总增广轮数 $\le |V|^{\frac{2}{3}}$。

自己整吧，假设进行了 $2|V|^{\frac{2}{3}}$ 次增广，证明边集大小不超过 $V|^{\frac{2}{3}}$，再转化为割。

最后，得出结论，在单位容量的网络上，Dinic 算法的总时间复杂度是 $O(|E| \min(|E|^\frac{1}{2}, |V|^{\frac{2}{3}}))$。

Push-Relabel 预流推进算法

该方法在求解过程中忽略流守恒性，并每次对一个结点更新信息，以求解最大流。

你不会以为我要讲吧。

LBY 提供了一个卡常或者叫做神奇常数优化小技巧来通过模板题，具体参考他的网络流与二分图详解。

但是我闲得慌，其实这个也不难，所以我就提一嘴主要思想，我是不会实现的。

首先，我们注意到其他的算法都是 $O(n^2m),(n^3)$ 或 $O(nm^2)$ 等的时间复杂度，太大了，有没有更加紧凑的时间复杂度上界呢？有的，兄弟有的，预流推进的优化 HLPP 时间复杂度为 $O(n^2m^{\frac{1}{2}})$，快多了，而且在随机图中也不劣于前面的 Dinic 或者优化了的 ISAP（想要了解可以自行搜索，相较于 Dinic 优化了常数）。

现在，我们管它能不能塞那么多，源点直接全部流出去。预流推进算法的思想就是，允许水在非源汇点的节点中暂时存储（我们将存储在非源汇点中的流称作这个点的超额流），同时伺机将自身的超额流通过管道推送出去。只要保证在算法结束后所有非源汇点的超额流都为0，那么这种方案就是合法的。

为了防止两个节点来回推流，我们先设置一个高度函数 $h(x)=0$。

推流：如果结点 $u$ 溢出，且存在结点 $v((u,v)\in E_f,c(u,v)-f(u,v)>0,h(u)=h(v)+1)$，那么我们尽可能将超额流从 $u$ 推送到 $v$，推送过程中我们只关心超额流和 $c(u,v)-f(u,v)$ 的最小值，不关心 $v$ 是否溢出，如果 $(u,v)$ 在推送完之后满流，将其从残量网络中删除。

具体的呢，就是如下操作。

1. 先从s向周围点推流（把该点的超额流推给周围点，注意：推的流量不能超过边的容量也不能超过该点超额流），并让周围点入队（ **注意：s 和 t 不能入队 **）

2. 不断地取队首元素，对队首元素推流

3. 队列为空时结束算法，$t$ 点的超额流即为最大流。

同时，我们在过程中要检查是否有结点 $u$ 溢出，且 $\forall (u,v)\in E_f,h(u)\leq h(v)$，那么我们就要将 $h(u)$ 更新为 $\min_{(u,v)\in E_f}h(v)+1$。

为什么这样就不会出现来回推流的情况了呢？

当两个点开始来回推流时，它们的高度会不断上升，当它们的高度大于 $s$ 时，会把超额流还给 $s$。

所以在开始预流推进前要先把s的高度改为n（点数），免得一开始 $s$ 周围那些点就急着把超额流还给s。

简单吧，但是它时间常数太大了。

考虑优化（HLPP），本质上预流推进就是因为推流和重标号次数太多了，那我们考虑减少它们的次数。

1. 先从 $t$ 到 $s$ 反向 BFS，使每个点有一个初始高度

2. 从 $s$ 开始向外推流，将有超额流的点放入优先队列

3. 不断从优先队列里取出高度最高的点进行推流操作

4. 若推完还有超额流，更新高度标号，重新放入优先队列

5. 当优先队列为空时结束算法，最大流即为 $t$ 的超额流

显然，我们还想继续优化，于是我们注意到如果某个高度不存在，为什么我们还要继续算？直接将所有比该高度高的节点标记为不可到达（使它的高度为 $n+1$，这样就会直接向 $s$ 推流了）。

最小割

但是，现在老师们要去堵住学生们，不让他们抢饭，所以要出动一些老师去堵住通道（物理意义），但是老师显然是有限的，于是我们想要知道要多少个老师才可以堵完学生，不让他们吃饭（一个也不能放过）

这就是最小割。

因为有最大流最小割定理，所以我们可以直接求出最大流即为最小割。

最小费用最大流

算法介绍

现在，我们黑心的学校给出了每条楼道的通过价格，每个人通过时都得交钱，所以我们要去求出在有最多人第一时间赶到的时候最少要花多少钱。

这就是最小费用最大流。

那么它应该怎么解决呢？我们看一眼，发现原来 Dinic 算法中有一个寻找增广路的过程，那么我们直接将这个寻找增广路的过程替换为寻找最短路的过程。

结束……了吗？

不对啊，这里会有负权回路的啊！那这样的话什么最短路都不行了啊。于是，我们现在有两种思路。

第一种，我们既然不能处理负环，那就直接不处理，让图里没有负环不就行了。

这就是消圈算法：（不总结）。

第二种，干脆点，我们直接没有负权边不就行了。

所以我们提前让负权边满流，那么图里不就全是正权了吗，又因为最大流本来就有『反悔』这一性质，于是我们这样做是正确的。

参考代码

#include
#define int long long
using namespace std;
const int inf = 1145141919810ll;
struct Edge {
	int v, w, c, nxt;
	Edge(int v = 0, int w = 0, int c = 0, int nxt = 0) :v(v), w(w), c(c), nxt(nxt) {}
}edge[100000 + 10];
int head[5000 + 10], idx = 1;
void add(int u, int v, int w, int c) {
	edge[++idx] = { v,w,c,head[u] };
	head[u] = idx;
}
int n, m, s, t, dis[5000 + 10], cur[5000 + 10];
bool vis[5000 + 10];
bool bfs() {
	memset(vis, 0, sizeof vis);
	queueq;
	for (int i = 1; i <= n; ++i) dis[i] = inf, cur[i] = head[i];
	dis[s] = 0; q.push(s); vis[s] = 1;
	bool flg = 0;
	while (!q.empty()) {
		int now = q.front(); q.pop(); vis[now] = 0;
		flg |= now == t;
		for (int i = head[now]; i; i = edge[i].nxt) {
			int& v = edge[i].v;
			if (dis[v] > dis[now] + edge[i].c && edge[i].w > 0) {
				dis[v] = dis[now] + edge[i].c;
				if (!vis[v])
					q.push(v),
					vis[v] = 1;
			}
		}
	}
	return flg;
}
int ans;
int dfs(int x, int flow) {
	if (x == t) return flow;
	vis[x] = 1;
	int ans = 0;
	for (int& i = cur[x]; i && flow; i = edge[i].nxt) {
		int& v = edge[i].v;
		if (!vis[v] && edge[i].w > 0 && dis[v] == dis[x] + edge[i].c) {
			int k = dfs(v, min(flow, edge[i].w));
			if (k == 0) dis[v] = inf;
			edge[i].w -= k;
			edge[i ^ 1].w += k;
			ans += k; flow -= k;
			::ans += k * edge[i].c;
		}
	}
	vis[x] = 0;
	return ans;
}
signed main() {
	cin.tie(0)->sync_with_stdio(false);
	cin >> n >> m >> s >> t;
	for (int i = 1, u, v, w, c; i <= m; ++i)
		cin >> u >> v >> w >> c, add(u, v, w, c), add(v, u, 0, -c);
	int ans = 0;
	while (bfs()) ans += dfs(s, inf);
	cout << ans << ' ' << ::ans << endl;
	return 0;
}

模拟费用流

算法介绍

对于有的题目，我们没有办法直接跑费用流，但是图十分有规律，所以我们手动模拟一下费用流的阶段。

这就是模拟费用流。

模拟费用流通过分析问题结构，模拟网络流的增广过程，避免显式建图。常用于特殊结构问题，如带权匹配、资源分配等。其核心是维护决策的优先队列，模拟费用流的贪心选择过程。

典型应用场景如"Poor Students"问题：$n$个学生选择$k$种课程，每个课程有容量限制，学生选择不同课程产生不同费用，要求总费用最小。

参考代码

#include
#define int long long
using namespace std;
const int inf = 1145141919810ll;
int dis[20 + 5], edge[20 + 5], fa[20 + 5];
bool vis[20 + 5], notdel[20 + 5][100000 + 5];
set> edges[20 + 5][20 + 5];
int c[100000 + 5][20 + 5], cnt[20 + 5], n, k;
int spfa() {
	memset(vis, 0, sizeof vis);
	memset(dis, 0x3f, sizeof dis);
	queue q; q.push(0);
	vis[0] = 1; dis[0] = 0;
	while (!q.empty()) {
		int now = q.front(); q.pop();
		vis[now] = 0;
		for (int v = 0; v <= k; v++) {
			if (edges[now][v].size()) {
				int w = edges[now][v].begin()->first, id = edges[now][v].begin()->second;
				if (dis[v] > dis[now] + w) {
					dis[v] = dis[now] + w;
					fa[v] = now; edge[v] = id;
					if (!vis[v])
						q.push(v), vis[v] = 1;
				}
			}
		}
	}
	int id = -1;
	for (int i = 1; i <= k; ++i)
		if (cnt[i] > 0 && (id == -1 || dis[i] < dis[id]))
			id = i;
	return id;
}
signed main() {
	ios::sync_with_stdio(false);
	cin >> n >> k;
	for (int i = 1; i <= n; ++i) {
		c[i][0] = inf; notdel[0][i] = 1;
		for (int j = 1; j <= k; j++)
			cin >> c[i][j], edges[0][j].insert({ c[i][j] - inf,i });
	}
	for (int i = 1; i <= k; ++i) cin >> cnt[i];
	int ans = 0;
	for (int T = n; T; --T) {
		int v = spfa();
		cnt[v]--;
		ans += dis[v];
		while (v) {
			int now = fa[v], w = edge[v];
			for (int i = 0; i <= k; ++i) {
				if (i != now) {
					if (!notdel[i][w]) edges[now][i].erase({ c[w][i] - c[w][now],w });
					else edges[i][now].insert({ c[w][now] - c[w][i],w });
				}
			}
			for (int i = 0; i <= k; ++i) {
				if (i != v) {
					if (notdel[i][w]) edges[i][v].erase({ c[w][v] - c[w][i],w });
					else edges[v][i].insert({ c[w][i] - c[w][v],w });
				}
			}
			edges[now][v].erase({ c[w][v] - c[w][now],w });
			edges[v][now].insert({ c[w][now] - c[w][v],w });
			notdel[now][w] ^= 1; notdel[v][w] ^= 1;
			v = now;
		}
	}
	cout << ans + n * inf << '\n';
	return 0;
}

上下界网络流

无源汇上下界可行流

算法介绍

要求构造满足以下条件的流：

1. 容量限制：$l(u,v) \leq f(u,v) \leq r(u,v)$
2. 流量守恒：$\sum_v f(u,v) = \sum_v f(v,u),\ \forall u$

解法：

1. 建立超级源点$S'$和超级汇点$T'$
2. 对原边$u→v$，建边$u→v$，容量$r-l$，记录下界$l$
3. 计算每个点的流量差$d(u)=\sum (入边下界) - \sum (出边下界)$
4. 若$d(u)>0$，建边$S'→u$，容量$d(u)$；否则建边$u→T'$，容量$-d(u)$
5. 跑$S'→T'$的最大流，若满流则可行

参考代码

#include
#define int long long
using namespace std;
const int inf = 1145141919810ll;
struct Edge {
	int v, w, nxt;
	Edge(int v = 0, int w = 0, int nxt = 0) :v(v), w(w), nxt(nxt) {}
}edge[100000 + 10];
int head[1000 + 10], idx = 1;
void add(int u, int v, int w) {
	edge[++idx] = { v,w,head[u] };
	head[u] = idx;
}
void addedge(int u, int v, int w) {
	add(u, v, w); add(v, u, 0);
}
int n, m, s, t;
int dis[1000 + 10];
int cur[1000 + 10];
bool bfs() {
	queueq;
	for (int i = 1; i <= n; ++i) dis[i] = inf, cur[i] = head[i];
	dis[s] = 0;
	q.push(s); bool flg = 0;
	while (!q.empty()) {
		int now = q.front(); q.pop();
		flg |= now == t;
		for (int i = head[now]; i; i = edge[i].nxt) {
			int& v = edge[i].v;
			if (dis[v] == inf && edge[i].w > 0)
				q.push(v), dis[v] = dis[now] + 1;
		}
	}
	return flg;
}
int dfs(int x, int flow) {
	if (x == t) return flow;
	int ans = 0;
	for (int& i = cur[x]; i; i = edge[i].nxt) {
		int& v = edge[i].v;
		if (edge[i].w > 0 && dis[v] == dis[x] + 1) {
			int k = dfs(v, min(flow, edge[i].w));
			if (k == 0) dis[v] = inf;
			edge[i].w -= k;
			edge[i ^ 1].w += k;
			ans += k; flow -= k;
		}
	}
	return ans;
}
int d[1000 + 10], cbcyc[100000 + 10];
signed main() {
	cin.tie(0)->sync_with_stdio(false);
	cin >> n >> m; s = n + 1; t = n + 2;
	for (int i = 1, u, v, l, r; i <= m; ++i)
		cin >> u >> v >> l >> r, addedge(u, v, r - l), d[u] -= l, d[v] += cbcyc[idx] = l;
	for (int i = 1; i <= n; ++i)
		if (d[i] > 0) addedge(s, i, d[i]);
		else addedge(i, t, -d[i]);
	int ans = 0; n += 2;
	while (bfs()) dfs(s, inf);
	bool cbc = 1;
	for (int i = head[s]; i; i = edge[i].nxt) cbc &= edge[i].w == 0;
	if (cbc) {
		cout << "YES" << endl;
		for (int i = 3, j = 1; j <= m; i += 2, j++) cout << edge[i].w + cbcyc[i] << endl;
	}
	else {
		cout << "NO" << endl;
	}
	return 0;
}

有源汇上下界可行流

算法介绍

在无源汇基础上，允许源点$s$净流出，汇点$t$净流入。解决方法：

1. 添加边$t→s$，容量$+\infty$
2. 转化为无源汇可行流问题，若存在可行流，则$t→s$边的流量即为原图可行流流量

有源汇上下界最大流

算法介绍

在可行流基础上，求最大流：

1. 先求可行流，若不存在则结束
2. 删除$t→s$的无穷边，在残量网络上跑$s→t$的最大流
3. 最终流量=可行流流量 + 新增流量

有源汇上下界最小流

算法介绍

在可行流基础上，求最小流：

1. 先求可行流，若不存在则结束
2. 删除$t→s$的无穷边，在残量网络上跑$t→s$的最大流
3. 最终流量=可行流流量 - 回退流量

上下界网络流

结合图理解一下吧。

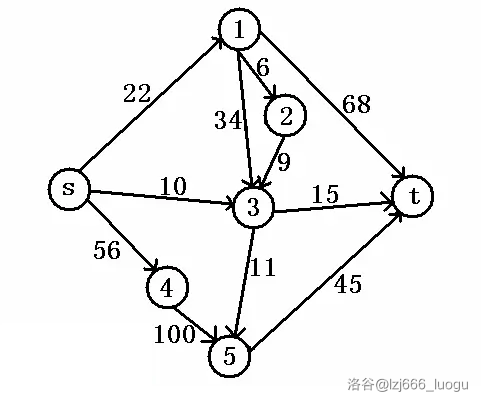
接下来就是一些定义了。

网络（$network$）是指一个特殊的有向图 $G=(V,E)$，其与一般有向图的不同之处在于有容量和源汇点。

$E$ 中的每条边 $(u, v)$ 都有一个被称为容量（$capacity$）的权值，记作 $c(u, v)$。当 $(u,v)\notin E$ 时，可以假定 $c(u,v)=0$。

$V$ 中有两个特殊的点：源点（$source$）$s$ 和汇点（$sink$）$t$（$s \neq t$）。

对于网络 $G=(V, E)$，流（$flow$）是一个从边集 $E$ 到整数集或实数集的函数，其满足以下性质。

容量限制：对于每条边，流经该边的流量不得超过该边的容量，即 $0 \leq f(u,v) \leq c(u,v)$；
流守恒性：除源汇点外，任意结点 $u$ 的净流量为 $0$。其中，我们定义 $u$ 的净流量为 $f(u) = \sum_{x \in V} f(u, x) - \sum_{x \in V} f(x, u)$。
对于网络 $G = (V, E)$ 和其上的流 $f$，我们定义 $f$ 的流量 $|f|$ 为 $s$ 的净流量 $f(s)$。作为流守恒性的推论，这也等于 $t$ 的净流量的相反数 $-f(t)$。

对于网络 $G = (V, E)$，如果 $\{S, T\}$ 是 $V$ 的划分（即 $S \cup T = V$ 且 $S \cap T = \varnothing$），且满足 $s \in S, t \in T$，则我们称 $\{S, T\}$ 是 $G$ 的一个 $s-t$ 割（$cut$）。我们定义 $s-t$ 割 $\{S, T\}$ 的容量为 $||S, T|| = \sum_{u \in S} \sum_{v \in T} c(u, v)$。

摘自 OI Wiki。

不算太抽象，可以理解。

例题讲解

P3376 【模板】网络最大流

板子。加强版在这里：P4722 【模板】最大流 加强版 / 预流推进。

P2766 最长不下降子序列问题

观察到 $n\le500$，我们考虑 $O(n^2)$ 的 DP 是怎么处理的。

第一问简单。

我们观察这个 $f$ 数组，它长得十分好看，于是我们考虑利用 $f$ 数组的转移建立一张图，求解答案。

现在，我们新建一个虚拟的源点和汇点，容易发现我们的目的是把每一个 LIS 表示成一条从源点到汇点的弧，同时保证每个点只用一次。可以考虑把每个点拆开，将点 $c$ 拆成两个点 $c_{in},c_{out}$，分别表示这个点的入源和出源，因为需要保证每个点只用一次嘛。

接下来，从源点向 $f_c=1$ 的点 $c_{in}$ 建边，从 $f_c=n$ 的 $c_{out}$ 向汇点建边，当然，还要从所有 $c_{in}$ 向 $c_{out}$ 建边。

直接跑一遍就是第二问的答案。

观察到第三问允许在取出的序列中多次使用 $x_1$ 和 $x_n$，所以我们发现将 $\{s,1_{in}\},\{1_{in},1_{out}\},\{n_{in},n_{out}\},\{n_{out},t\}$ 的流直接改成 $inf$ 就可以了。

P2598 狼和羊的故事

最小割板子。

建图方式：

1. 原点向所有狼连流量 $inf$ 的边（显然不能被割了）

2. 所有羊向汇点连流量 $inf$ 的边（同理）

3. 所有点向四周连流量为 $1$ 的边（看割几条就等同于建几个栅栏）

没了。

T390029 0x69-网络流初步-有线电视网 - 洛谷

也是最小割。

考虑如何将原图转化成最小割。

首先，我们发现如果把一个点拆成入点和出点，那么断裂掉入点和出点的链接就相当于删去了这个点，也就实现了点转边。

于是拆点，将每个点都从入点连一条权值为 $1$ 的边向出点，将原图上的边权值设为 $inf$（防止被割断），然后可以直接求最小割。

注意结果要对 $n$ 取 $\min$。

练习题