字符串问题略解

前言

由于本人太久没复习 KMP 了，复习好像重学了一遍，在这里写个博客来记录一下。

另：还有其他字符串算法，一并整理了算了。

KMP

初学时好像挺蒙，只觉得好像那样，实际上它确有精妙之处。

首先定义一个 $border$ 数组为匹配串前 $i$ 位的最长公共前后缀（不算它自己）长度（同时也是前缀结束位置）为 $border_i$。

考虑如何去求 $border$：

假设当前处理到第 $i$ 位，那么前 $i-1$ 位的都已经处理好了，对于第 $i-1$ 位的 $border$，我们发现可以考虑加上一位构成我们新的 $border$，但是如果失配呢？

由于 $border$ 为最长公共前后缀，所以它是前面的等于后面的，考虑取前面的前缀与后面的后缀来进行新的匹配。

来个图吧。

a	b	a	b	$\color{red}{a}$
a	b	a	b	a	b	c
		a	b	a	b	$\color{red}{c}$

假设处理到第 $7$ 位了，那么我们试图使用前面（第 $6$ 位）的 $border$ 来匹配。

ababa $\not =$ ababc

考虑取前面的前缀与后面的后缀来进行新的匹配。

a	b	$\color{red}{a}$
a	b	a	b	a	b	c
				a	b	$\color{red}{c}$

反正都是一样的串，又是公共前后缀，所以肯定一样啊，又取的最长，所以正确性也有了保障。

还是失配怎么办？接着取 $border$ 就行了啊。

再举个例子。

a	b	c	a	b	$\color{red}{a}$
a	b	c	a	b	a	a	b	c	a	b	c
						a	b	c	a	b	$\color{red}{c}$

考虑取前面的前缀与后面的后缀来进行新的匹配。

a	b	$\color{red}{c}$
a	b	c	a	b	a	a	b	c	a	b	c
									a	b	$\color{red}{c}$

匹配上了！这就是它的 $border$。

同理，去用匹配串取匹配待匹配串，如果失配了，那么就跳到 $border$ 继续尝试。

为什么可以减小时间复杂度呢？其实还是因为有了 $border$，也就是失配数组，减少了重复冗余的比较。

AC 自动机

trie 树会吧，在此基础上我们加一堆边。

定义回跳边为当前节点的在树边（原来的 trie 树边）上的父亲节点的回跳边所指的节点的与自己同一方向的儿子（没有的就指到根节点）。

有点绕，来张图。

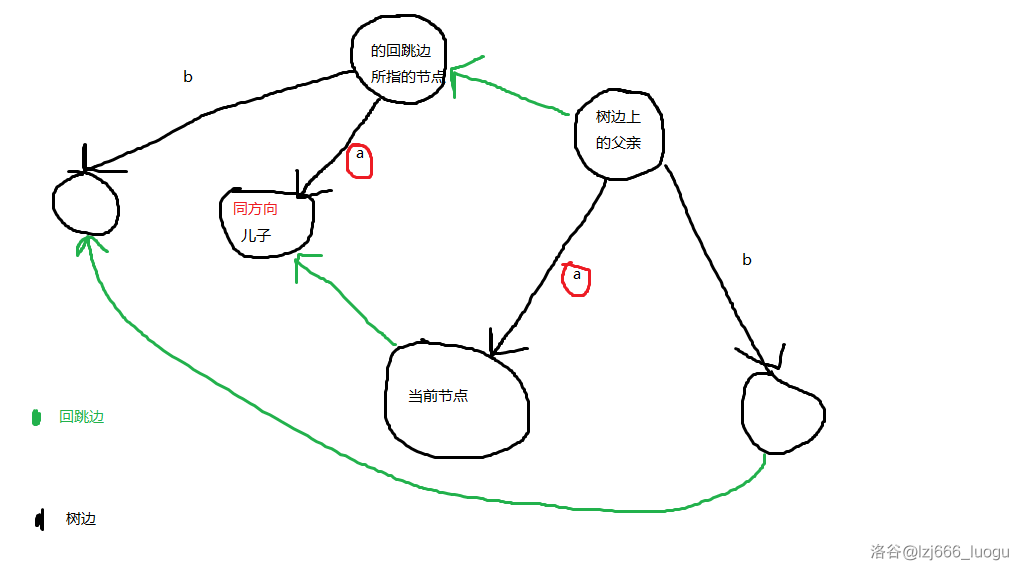
所以呢？它究竟代表什么呢？

观察下面这张图：

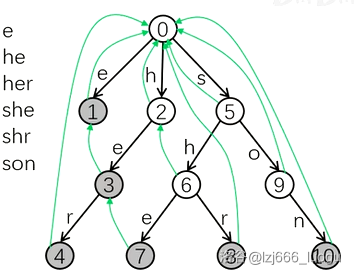
容易发现回跳边所指的节点代表的字符串为它在这个 trie 树上的最长后缀。

定义转移边为一个节点的回跳边所指的节点的与自己同一方向的儿子（没有的就指到根节点）。

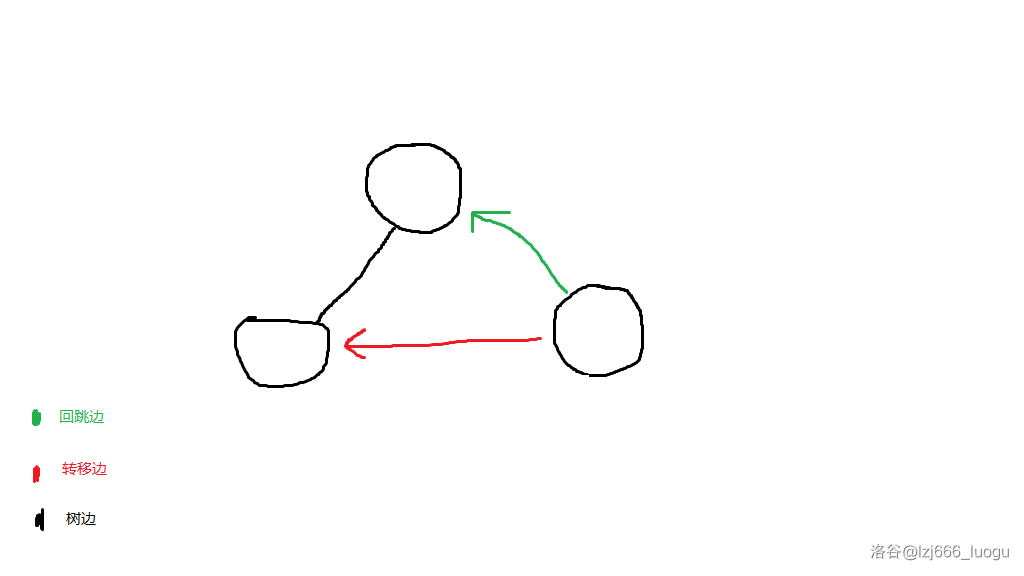
容易发现转移边所指的节点代表的字符串为它在这个 trie 树上的有最长公共（它的）前（我的）后缀的串。

所以在主串匹配的时候就不断走树边（正常扩展）和转移边（失配），而每到一个节点就把由回调边组成的从它到根节点的链上的所有节点都统计一遍，就是答案了。

优化：如果只统计出现的串的个数就给每个节点打上标记，如果统计次数的话就将每个起始点出现次数加加，最后再统一用 topo 遍历一遍回跳边层层扩展上去就行了。

时间复杂度还是 $O(n + m)$ 的。