莫队

配套资料（？）

题单：https://www.luogu.com.cn/training/664944#information

参考代码：/paste/929v6j2g

来源

话说，彼时的 OI 界 RMQ 问题并起，而我们的暴力却不能骗到太多分，于是 CF 高手圈内流行起了一种快速处理离线问题的算法，并由莫涛整理，这种算法便被称之为莫队。后人便在此基础上加以拓展，统称为莫队算法。

普通莫队

应用范围

假设 n, m 同阶，那么对于序列上的区间询问问题，如果从 [l, r] 的答案能够 O(1) 扩展到 [l − 1, r], [l + 1, r], [l, r + 1], [l, r − 1]（即与 [l, r] 相邻的区间）的答案，那么莫队可以在 $O(n\sqrt{n})$ 的复杂度内求出所有询问的答案。

原理

双指针左右横跳跳跃。

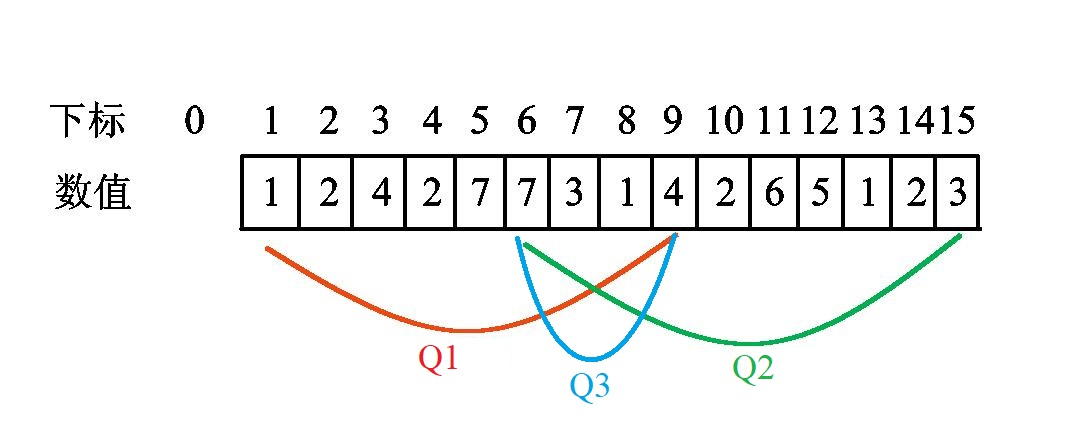
以这张图为例，我们要在 Q1 和 Q2 两个询问间转移，怎么转移呢？

假设我们已经求出了 Q1 的答案，我们只需要干 2 步。

1. 左指针右移，求出 Q3 的答案。（删除操作）
2. 右指针右移，求出 Q2 的答案。（增加操作）

那么如何从 Q2 求到 Q1 呢？

还是如此。

1. 右指针左移，求出 Q3 的答案。（删除操作）
2. 左指针左移，求出 Q1 的答案。（增加操作）

于是，我们将 1 操作成为加入操作，2 操作称为删除操作，莫队中的加入和删除操作是解决问题的核心，一般来说加入和删除操作的时间复杂度得小，大多数情况下得确保它是 O(1) 的。

具体怎么实现呢？我们来看一道例题。

https://www.luogu.com.cn/problem/P3901

只看怎么实现加入和删除操作的话，我们可以观察到值域只有 10⁵，考虑用一个桶来维护，再维护一个出现次数超过 1 次的数的个数就行了。

代码：

int vis[100000 + 10], a[100000 + 10], sum;
void ins(int x) {
	if (vis[a[x]] == 1)
		sum++;
	vis[a[x]]++;
}
//加入操作
void del(int x) {
	vis[a[x]]--;
	if (vis[a[x]] == 1)
		sum--;
}
//删除操作

那么这样，我们就可以做出这道题了……（吗？）

不对啊，这样暴力跳，很明显会被卡到 O(n²) 啊？

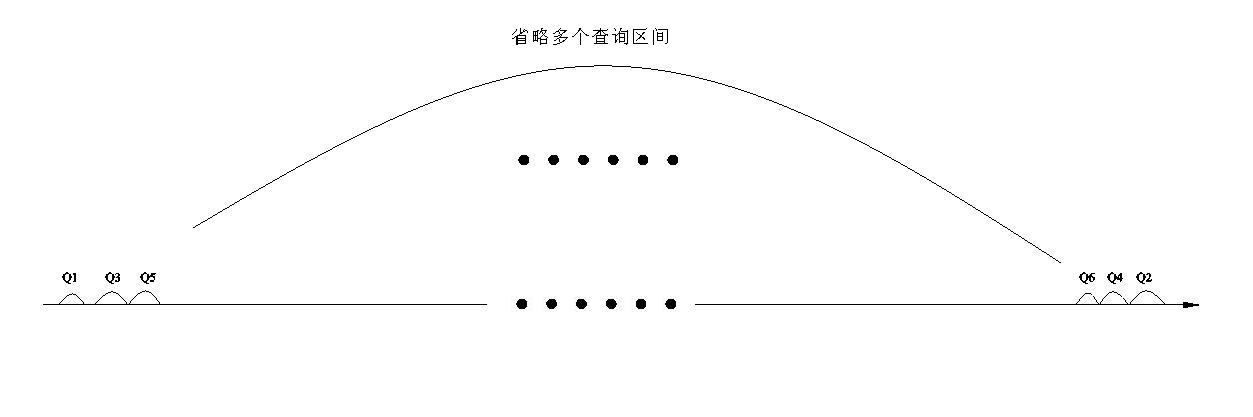
莫队算法伪掉了，不用学了。

再对着这个图看一眼，诶，我们发现从 Q1 到 Q3 到 Q5 等等的转移其实代价很小，所以我们自然的想到一个技巧：重排询问！

所以到底怎么弄呢，我们可以考虑把所有查询区间按左端点排序，从而使左指针最多移动 O(n) 次。但这样的话右端点又是无序的，右指针又让整体复杂度打回原形。看上去，这个复杂度已经不能再优化了。

于是，一个非常神奇的点出现了，莫队的重排询问机制。

先说怎么做，首先我们先这 n 个点顺序平均分成 $\sqrt{n}$ 个块，然后询问间排序时以左端点所在的块编号为第一关键字，右端点为第二关键字。

嗯？这样就能优化了吗？

证：令每一块中 L 的最大值为 $\max_1,\max_2,\max_3, \cdots , \max_{\lceil\sqrt{n}\rceil}$。

由第一次排序可知，$\max_1 \le \max_2 \le \cdots \le \max_{\lceil\sqrt{n}\rceil}$。

显然，对于每一块暴力求出第一个询问的时间复杂度为 O(n)。

考虑最坏的情况，在每一块中，R 的最大值均为 n，每次修改操作均要将 L 由 max_i − 1 修改至 max_i 或由 max_i 修改至 max_i − 1。

考虑 R：因为 R 在块中已经排好序，所以在同一块修改完它的时间复杂度为 O(n)。对于所有块就是 $O(n\sqrt{n})$。

重点分析 L：因为每一次改变的时间复杂度都是 O(max_i − max_i − 1) 的，所以在同一块中时间复杂度为 $O(\sqrt{n}\times(\max_i-\max_{i-1}))$。

将每一块 L 的时间复杂度合在一起，可以得到：

对于 L 的总时间复杂度为

$$ \begin{aligned} & O(\sqrt{n}(\max{}_1-1)+\sqrt{n}(\max{}_2-\max{}_1)+\sqrt{n}(\max{}_3-\max{}_2)+\cdots+\sqrt{n}(\max{}_{\lceil\sqrt{n}\rceil}-\max{}_{\lceil\sqrt{n}\rceil-1))} \\ = \phantom{} & O(\sqrt{n}\times(\max{}_1-1+\max{}_2-\max{}_1+\max{}_3-\max{}_2+\cdots+\max{}_{\lceil\sqrt{n}\rceil-1}-\max{}_{\lceil\sqrt{n}\rceil-2}+\max{}_{\lceil\sqrt{n}\rceil}-\max{}_{\lceil\sqrt{n}\rceil-1)}) \\ = \phantom{} & O(\sqrt{n}\times(\max{}_{\lceil\sqrt{n}\rceil-1}))\\ \end{aligned} $$ （裂项求和）

由题可知 $\max_{\lceil\sqrt{n}\rceil}$ 最大为 n，所以 L 的总时间复杂度最坏情况下为 $O(n\sqrt{n})$。

于是就得出了总时间复杂度 $O(n\sqrt{n}+n\sqrt{n}+n\log{n})=O(n\sqrt{n})$。

但是对于 m 的其他取值，如 m < n，分块方式需要改变才能变的更优。

怎么分块呢？

我们设块长度为 S，那么对于任意多个在同一块内的询问，挪动的距离就是 n，一共

$\displaystyle \frac{n}{S}$ 个块，移动的总次数就是 $\displaystyle \frac{n^2}{S}$，移动可能跨越块，所以还要加上一个 mS 的复杂度，总复杂度为 $\displaystyle O\left(\frac{n^2}{S}+mS\right)$，我们要让这个值尽量小，那么就要将这两个项尽量相等，发现 S 取 $\displaystyle \frac{n}{\sqrt{m}}$ 是最优的，此时复杂度为

$$ O\left(\frac{n^2}{\displaystyle \frac{n}{\sqrt{m}}}+m\left(\frac{n}{\sqrt{m}}\right)\right)=O(n\sqrt{m})。 $$

事实上，如果块长度的设定不准确，则莫队的时间复杂度会受到很大影响。例如，如果 m 与 $\sqrt n$ 同阶，并且块长误设为 $\sqrt n$，则可以很容易构造出一组数据使其时间复杂度为 $O(n \sqrt n)$ 而不是正确的 O(n)。

那么这样，我们就可以做出这道题了吧。

例题

https://www.luogu.com.cn/problem/P1494

考虑如何实现加入和删除，观察到实际取到两只相同颜色袜子的方案数就是 $\displaystyle \sum_{i=1}^{n} (cnt_i-1) \times cnt_i$，每次加入删除只有一个对应颜色的出现次数被修改了，考虑维护一个答案 sum 先减去原来的 (cnt_i − 1) × cnt_i ，再令 cnt_i ← cnt_i ± 1，重新累加贡献就行了。

局限性

只能离线，不能带修之类的；只能处理区间问题；必须得答案支持加入和删除可以小时间复杂度实现。

带修莫队

普通莫队是不能带修改的。

我们可以强行让它可以修改，就像 DP 一样，可以强行加上一维 时间维, 表示这次操作的时间。

时间维表示经历的修改次数。

即把询问 [l, r] 变成 [l, r, time]。

那么我们的坐标也可以在时间维上移动，即 [l, r, time] 多了一维可以移动的方向，可以变成：

$$ [l-1,r,\text{time}]\\ [l+1,r,\text{time}]\\ [l,r-1,\text{time}]\\ [l,r+1,\text{time}]\\ [l,r,\text{time}-1]\\ [l,r,\text{time}+1] $$

这样的转移也是 O(1) 的，但是我们排序又多了一个关键字，再搞搞就行了。

但是这样的话块的大小也需要重新调整。

通过一通我不懂的证明，当块长取 $\dfrac{\sqrt[3]{n^{2}}\sqrt[3]{t}}{\sqrt[3]{m}}$ 时有最优时间复杂度 $O\left(\sqrt[3]{n^{2}}\sqrt[3]{m^{2}}\sqrt[3]{t}\right)$。

常说的 $O\left(n^{\frac{5}{3}}\right)$ 便是把 n, m, t 当做同数量级的时间复杂度。

实际操作中还是推荐设定 $n^{\frac{2}{3}}$ 为块长。

例题

https://www.luogu.com.cn/problem/P1903

就和 https://www.luogu.com.cn/problem/P3901 很像吧（甚至数字都一样），只需要加一维时间就行了嘛。

局限性

只能单修，只比暴力优化了一个 $n^{\frac{1}{3}}$，但是毕竟优化了。本质上还是离线。

回滚莫队

有些题目在区间转移时，可能会出现增加或者删除无法实现的问题。在只有增加不可实现或者只有删除不可实现的时候，就可以使用回滚莫队在 $O(n \sqrt m)$ 的时间内解决问题。回滚莫队的核心思想就是：既然只能实现一个操作，那么就只使用一个操作，剩下的交给回滚解决。

观察一道例题：https://www.luogu.com.cn/problem/AT_joisc2014_c

形式化：给你一个长度为 n 的数组 A 和 m 个询问 (1 ≤ n, m ≤ 10⁵)，每次询问一个区间 [L, R] 内重要度最大的数字，要求：输出其重要度。一个数字 i 重要度的定义为 i 乘上 i 在区间内出现的次数。

在这个问题中，在增加的过程中更新答案是很好实现的，但是在删除的过程中更新答案是不好实现的。因为如果增加会影响答案，那么新答案必定是刚刚增加的数字的重要度，而如果删除过后区间重要度最大的数字改变，我们很难确定新的重要度最大的数字是哪一个。

于是使用回滚莫队，我们想普通莫队一样分块，排序，并设块的大小为 b。

对于每堆左端点在同一个块内的询问，我们分别进行考虑，这时的莫队区间的左端点初始化为这个块的右端点加 1, 将莫队区间的右端点初始化为这个块的右端点。

对于左右端点在同一个块中的询问，我们直接暴力扫描回答即可（这个显然是 O(b) 的）。

对于这堆询问中的每一个询问，不断扩展右端点直至莫队区间的右端点等于询问的右端点，因为右端点是排过序的，所以右端点的移动是 O(n) 的。

然后定义一个操作撤销，具体的，在这道题中指在桶中减去出现次数，而不管答案是否改变。

每次暴力向左找，不断扩展莫队区间的左端点直至莫队区间的左端点等于询问的左端点。

回答询问（记录答案）。

撤销莫队区间左端点的改动，使莫队区间的左端点回滚到这个块的右端点加 1。

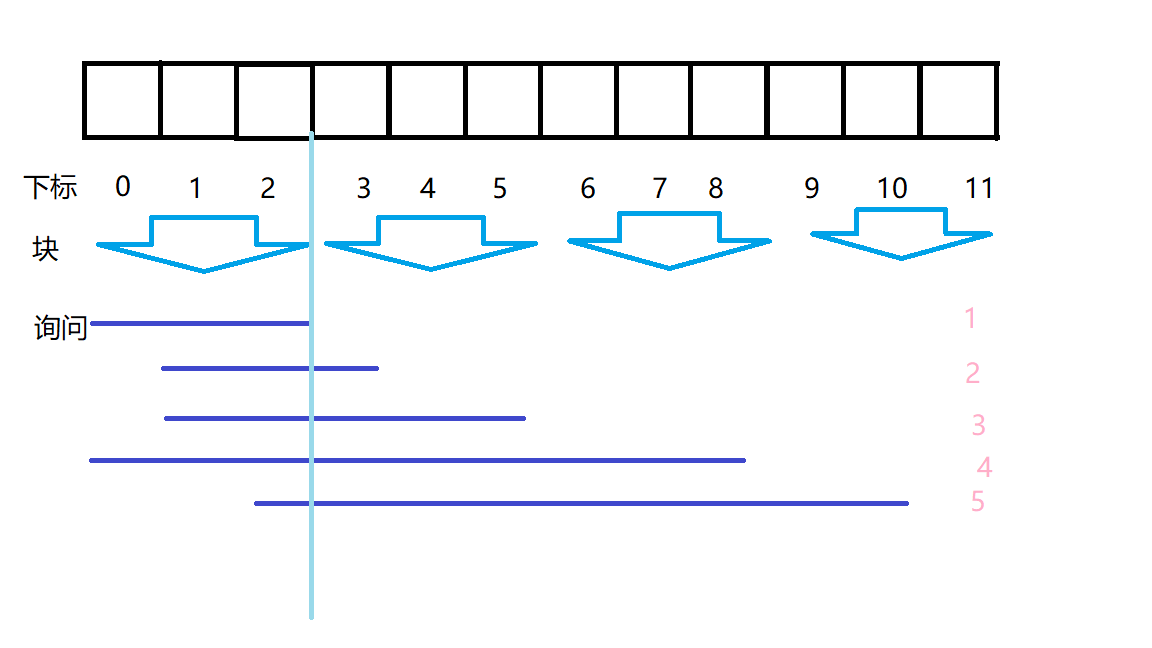
具体来分析吧。

对于 1 号询问，由于就是在块内，所以暴力处理。

对于 2 号询问，莫队区间先是右端点从 2 扩展到 3，然后左端点扩展到 1，记录答案，左端点重新回到 3。

对于 3 号询问，莫队区间先是右端点从 3 扩展到 5，然后左端点从 3 来到 1，记录答案，左端点重新回到 3。

对于 4 号询问，莫队区间先是右端点从 5 扩展到 8，然后左端点从 3 来到 0，记录答案，左端点重新回到 3。

对于 5 号询问，莫队区间先是右端点从 8 扩展到 10，然后左端点从 3 来到 2，记录答案，左端点重新回到 3。

时间复杂度是 $O(mb+\frac{n^2}{b})$，取 $b=\frac{n}{\sqrt{m}}$ 最优，时间复杂度为 $O(n\sqrt{m})$。

局限性

只能是可以支持一个操作的，并且答案得可以快速覆盖。

树上莫队

这年头，啥数据结构都上得上个树，莫队也不例外。

但是莫队都是处理区间问题的啊，咋上树？

例题：https://www.luogu.com.cn/problem/P4074

形式化一小下，给你一棵树，树上第 i 个点颜色为 c_i，每次询问一条路径 u_i, v_i, 求这条路径上的 $\displaystyle \sum_{c}val_c\sum_{i=1}^{cnt_c}w_i$ 其中：val 表示该颜色的价值，cnt 表示颜色出现的次数，w 表示该颜色出现 i 次后的价值。

咋做？我不会啊。

我们考虑把树上的修改，查询换到序列上，于是我们就想到了一个……（未完待续）